Introduction
La troposphère et la stratosphère sont les deux couches inférieures de l'atmosphère. La troposphère s'étend de la surface jusqu'à environ 10 ou 15 kilomètres d'altitude. La stratosphère s'étend au delà, jusqu'aux environs de 40 kilomètres d'altitude. Comme le montre le schéma suivant, la température décroit sur l'épaisseur de la troposphère, passant d'environ 15°C en surface à environ -60°C au sommet de la troposphère. Puis la tendance de température s'inverse et dans la stratosphère la température connait une croissance. Ce petit schéma résume ces éléments :Nous allons nous concentrer sur le profil de température en troposphère particulièrement, et nous tenterons de l'expliquer et de le justifier. Dans cet article, nous allons aussi balancer beaucoup de gros mots, comme température potentielle, entropie, etc... Nous allons tenter de rester le plus simple possible et de vous donner une idée de la thermodynamique atmosphérique, et quelques trucs et astuces de prévisionnistes. Nous parlerons de température potentielle équivalente θe et de température pseudo-potentielle du thermomètre mouillé θ'w qui permettent en quelque sorte de coller une étiquette sur l'air en mouvement, mais qui en pratique ont également d'autres intérêt. Pour vous aider à vous y retrouver, chaque paragraphe sera précédé d'un petit résumé. Vous pourrez ainsi vous éviter la lecture des parties les plus ardues si le cœur vous manque. Ci-dessous, les différents liens reprennent le plan de l'article.
Introduction
Comment bien ranger (résumé)
Les gaz parfaits (résumé)
L'hyrostatisme (résumé)
Définition de la température potentielle (résumé)
Le gradient thermique adiabatique sec (résumé)
L'air humide (résumé)
Les θ'w et θe en pratique (résumé)
Conclusion (ouf !) (résumé)
Un complément sur l'entropie pour els courageux. (résumé)
De l'importance de bien ranger
Intuitivement, tout le monde comprend que pour ranger des objets de masses variées, on met le plus lourd au fond. Dans un panier de course ou un sac de picnic par exemple, personne ne mettra la bouteille d'eau au dessus du paquet de chips. Sur des étagères branlantes, personne ne mettra les objets les plus lourds en haut, de crainte de voir l'édifice verser. De même, pour ceux qui font de la randonnée, ils savent l'importance de bien ranger le sac à dos et de l'équilibrer. De même pour ceux qui portent des charges, il est plus simple de manière générale d'avoir le lourd en bas (et de ne pas se pencher en avant pour ne pas se péter le dos mais de plier les jambes...). Encore un autre exemple, les voitures de courses sont très basses pour essayer de baisser au maximum le centre de gravité et d'avoir la masse au plus près du sol possible. Les tout-terrains vont contre cette loi pour pouvoir faire du franchissement, mais du coup ils sont plus instables et moins performants. C'est donc un principe général de la physique, gravité oblige. Le lourd tend à couler et tombe plus facilement au fond du bocal que le léger. Autant ne pas aller contre cette tendance donc.
Faisons déjà une ouverture en direction de l'atmosphère. Nous savons que de l'air plus chaud est aussi de l'air plus léger. De manière générale, à quelques exceptions notables près (surtout à l'exception de la glace en fait...), un corps qui s'échauffe se dilate également (rien de grivois là dedans. Quoique ? ). Ainsi les corps plus chauds tendent à être plus léger pour un même volume. Remarque bête, mais on parle bien sûr de volume. Un kilogramme de plomb, cela pèse autant qu'un kilogramme de plume, et un kilogramme d'eau à 4°C pèse autant qu'un kilogramme d'eau à 99°C. Ce que nous disons, c'est que le corps est plus léger à volume constant. Ainsi, mettons exactement un kilogramme d'eau dans une casserole d'un litre, et chauffons ce kilogramme d'eau en laissant l'eau déborder librement, il ne resterait plus que 950 grammes dans la casserole Note 1. Dans une montgolfière par exemple, on chauffe de l'air. L'air chaud étant plus léger, cela provoque le soulèvement de l'aérostat. L'air suit cependant lui aussi le principe de laisser le lourd en bas, et tente de se ranger lui-même si nous pouvons dire, en laissant le lourd en bas et le léger au dessus.
Pour autant, dans l'atmosphère, la température décroît avec l'altitude. Ainsi, il fait en moyenne plus doux à Bruxelles qu'au sommet de l'Ardenne. Or l'air chaud est plus léger. Comment se fait-il donc que l'air chaud soit au fond du bocal ? L'air chaud ne devrait-il pas suivre l'effet montgolfière et s'envoler vers le sommet de la troposphère ?
Nous allons ainsi voir comment l'air se range lui même, et comment, contrairement aux apparences, l'air le plus lourd est bien au fond du bocal et l'air le plus léger en haut. En effet, l'air chaud n'est pas forcément celui qu'on croit...
Loi des gaz parfaits
L'atmosphère est considéré comme un gaz parfait. Nous allons donc expliquer ce qu'est un gaz parfait. L'équation (qui a une certaine "célébrité" en physique) est la suivante :
P * v = r * T
Les paramètres sont les suivants :
r = 288 J.kg-1.K-1 pour de l'air pas trop humide (environ, cela dépend de différents paramètres, la valeur peut notamment varier de une ou deux unités avec l'humidité)
P : pression, Pascal
v : volume massique, m3/kg (c'est l'inverse de la masse volumique, appelé densité plus couramment -physiquement ce n'est pas tout à fait rigoureux mais nous ne sommes pas là pour nous prendre la tête sur des détails-. Donc plus v est grand, plus l'air est "léger" et inversement au contraire de la densité)
T : température, Kelvin (ajouter 273.15 à la température en degrés Celsius pour avoir des Kelvin. Typiquement, 0°C est égal à 273.15 Kelvins)
Ceci dit, que signifie, en français clair et plein, cette équation ? Elle explique que l'air au final se comporte comme une biesse réception dans une salle pas très grande.
Pour un volume d'air, la pression est la tendance des molécules d'air à s'entrechoquer dans l'espace défini, la masse volumique explique le nombre de têtes de pipes qu'il y a dans l'espace défini. La température est l'énergie cinétique propre des molécules.
Prenons le cas où v est constant, donc que plus personne ne rentre. Pour une raison quelconque, si on réchauffe le volume d'air, les molécules se mettent à s'agiter. Et bien, en conséquence la pression montera d'un cran. Tout comme dans la réception, si l’alcool coule à flot et que la température monte d'un cran, les gens s'agitent plus et risquent de se marcher sur les pieds plus rapidement...
On va s'essayer à calculer un peu la masse volumique (ou la densité de l'air si certains préfèrent, en gros savoir si l'air est "lourd" ou "léger" ) pour voir, à différent niveau de pression et de température. Notons ϱ (rho) la masse volumique, inverse du volume massique (aucune surprise). La masse volumique indique directement si l'air est lourd ou léger effectivement :
ϱ = 1/v
ϱ = P / ( r*T )
Prenons différentes situations dans l'atmosphère. En premier lieu, en surface, la pression est d'environ 101 325 Pa et la température de 15°C soit 288 K. Donc :
ϱ = 101325 / ( 288 * 288 )
ϱ = 1.22 kg/m3
Au niveau 850 hPa, donc 85 000 Pa, vers 1 500 mètres, la température est en moyenne de 5°C, soit 278 K. Donc :
ϱ = 85000 / ( 288 * 273 )
ϱ = 1.06 kg/m3
Au niveau 500 hPa, donc 50 000 Pa, vers 5 500 mètres, la température est en moyenne de -20°C, soit 253 K. Donc :
ϱ = 50000 / ( 288 * 253 )
ϱ = 0.69 kg/m3
Au niveau 300 hPa, donc 30 000 Pa, vers 9 100 mètres, la température est en moyenne de -45°C, soit 228 K. Donc :
ϱ = 30000 / ( 288 * 228 )
ϱ = 0.46 kg/m3
Au niveau 200 hPa, donc 20 000 Pa, vers 11 600 mètres, la température est en moyenne de -55°C, soit 223 K. Donc :
ϱ = 20000 / ( 288 * 223 )
ϱ = 0.32 kg/m3
On se rend compte ainsi que l'atmosphère est malgré tout "bien rangée". L'air le plus lourd est stocké au fond du bocal, près de la surface. Et quand on monte en altitude, la masse volumique décroit, donc l'air est bien de plus en plus léger.
Hydrostatisme
L'hydrostatique est l'étude des fluides (hydro) immobiles (statiques). Vu que l'atmosphère est tout le temps en mouvement, on peut se demander ce que vient faire là cette théorie. Et bien en fait, même si l’atmosphère n'est jamais immobile, l'hydrostatisme est quand même très bien respecté. En effet, pour être rigoureux, l'hydrostatisme exprime l'équilibre entre force de pression et gravité. Cette hypothèse est vérifiée si les accélérations verticales sont faibles face à l'accélération de la pesanteur. En français clair et plein, l'air en moyenne est plus comparable à une bagnole sur l'autoroute, posée à une certaine vitesse ; que comparable à une voiture de rallye en train d'accélérer, de tourner, et de freiner en permanence. Le fait que les accélérations soient faibles simplifie grandement le problème (même si l'analogie s'arrête là et que les deux phénomènes ne sont pas directement comparables, on peut noter que dans une voiture de rallye on a un effet "essoreuse à salade" qui n'est pas présent dans une voiture posée à une vitesse constante. Même si à nouveau ce n'est pas directement comparable, de manière générale les accélérations et décélérations rajoutent de la complexité et des effets supplémentaires aux phénomènes).
L'équation de l'hydrostatisme est donc :
P = ϱ * g * h ( à prononcer " p égal Roger !!!! h " )
Pour ceux qui s’appellent Roger, c'est votre heure de gloire, votre nom se retrouve dans une équation de physique.
À grande échelle, l'atmosphère est hydrostatique. À grande échelle, l'atmosphère est bien rangée, avec l'air le plus lourd au fond du bocal et l'air le plus léger au sommet et il n'y a pas d'air chaud qui flotte. Cela implique aussi que les mouvements atmosphériques ne sont pas gouvernés par la densité de l'air (typiquement, au delà d'une distance de 10 - 20 kilomètres pour la dimension caractéristique l'air ne bouge plus à cause de sa densité). Dans les orages, qui sont effectivement de petite taille, l'approximation hydrostatique n'est plus vérifiée et les mouvements de l'air sont effectivement dûs à la densité. Dès qu'on dépasse une taille de 10 - 20 km, les mouvements de l'air ne sont cependant nullement dûs au fait que l'air chaud est lourd ou léger ou que l'air froid est lourd ou autre. C'est peut-être dommage ou malheureux, mais à grande échelle l'atmosphère est stable et les mouvements ne s'expliquent pas par "l'air chaud ça flotte, l'air froid ça coule". L'atmosphère est un peu plus compliqué que cela, pour le meilleur et pour le pire.
Température potentielle
Le premier gros mot est sorti, c'est la température potentielle, notée θ. C'est une lettre grecque se prononçant donc thêta, un peu comme un têtard qui a perdu sa Recherche & Développement (pour la petite blague, c'est un têtard, il croyait qu'il était tôt mais en fait il était tard...). Bref, fors les jeux de mots pourris, l'équation est la suivante :
θ = T * ( P / Préf )( r / Cp )
Cela peut faire peur, mais il n'y a rien de compliqué là dedans. Les paramètres sont essentiellement les mêmes :
T : température, Kelvin (ajouter 273.15 à la température en degrés Celsius pour avoir des Kelvin. Typiquement, 0°C est égal à 273.15 Kelvins)
P : pression, Pascal
r = 288 J.kg-1.K-1 (environ, cela dépend de différents paramètres, la valeur peut notamment varier de une ou deux unités avec l'humidité)
Cp = 1 005 J.kg-1.K-1 (environ, cela dépend des mêmes différents paramètres)
Préf = 1 000 hPa
mais il y a ici une astuce de peau-rouge :
r / Cp = 2 / 7
C'est plus simple, il n'y a pas d'unités, bref comme quoi la physique ce n'est pas toujours si terrible. Et donc :
θ = T * ( Préf / P )(2/7)
Ce qui n'est vrai que pour l'air cependant, précisons le bien.
Cette température potentielle représente en quelque sorte l'équilibre entre la pression et la température pour une particule d'air. Si une particule d'air s'élève, elle va se détendre et donc se refroidir (toujours rien que du très logique donc). Au contraire, si une particule d'air s'enfonce, elle va se comprimer et donc se réchauffer. On va lâcher un deuxième gros mot, on parle là d'entropie. La température potentielle représente en fait l'entropie de la particule.
On va se calculer la température potentielle à différents niveaux pour voir son comportement. Prenons les mêmes niveaux de référence. En premier lieu, en surface, la pression est d'environ 101 325 Pa et la température de 15°C soit 288 K. Donc :
θ = 288 * ( 100 000 / 101 325 )( 2 / 7 )
θ = 287 K
Soit 14°C. Au niveau 850 hPa, donc 85 000 Pa, vers 1 500 mètres, la température est en moyenne de 5°C, soit 278 K. Donc :
θ = 273 * ( 100 000 / 85 000 )( 2 / 7 )
θ = 291 K
Soit 18°C. Au niveau 500 hPa, donc 50 000 Pa, vers 5 500 mètres, la température est en moyenne de -20°C, soit 253 K. Donc :
θ = 288 * ( 100 000 / 50 000 )( 2 / 7 )
θ = 308 K
Soit 35°C. Au niveau 300 hPa, donc 30 000 Pa, vers 9 100 mètres, la température est en moyenne de -45°C, soit 228 K. Donc :
θ = 228 * ( 100 000 / 30 000 )( 2 / 7 )
θ = 322 K
Soit 48°C. Au niveau 200 hPa, donc 20 000 Pa, vers 11 600 mètres, la température est en moyenne de -55°C, soit 223 K. Donc :
θ = 288 * ( 100 000 / 20 000 )( 2 / 7 )
θ = 353 K
Soit 80°C. L'air de rien on vient de montrer que la température, au final, augmente avec l'altitude. Nous confirmons donc ce que nous disions, l'atmosphère est bien rangée. Nous allons regarder les données de l'atmosphère recalculées par un ordinateur. Il s'agit d'une coupe latitude-hauteur. En quelque sorte, on prend l'atmosphère comme une boule en papier qu'on replie et dont on regarde la tranche. Démonstration. On a une boule en papier :
 |
| Image d'une boule en papier dépliée sortie d'un site commerciale quelconque. |
On l'a replie :
 |
| Image d'une boule en papier repliée sortie d'un site commerciale quelconque |
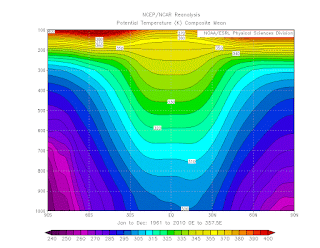 |
| Par rapport à l'étape précédente, on a simplement basculé la tranche de 90° vers la droite. Coupe latitude-verticale de al température potentielle, d'après la réanalyse NCEP-NCAR. Source : http://www.esrl.noaa.gov/psd/data/reanalysis/reanalysis.shtml |
À main gauche, le Pôle Sud, à main droite le Pôle Nord. Le plancher des vaches est en bas, le niveau 100 hPa en haut (vers 15 000 mètres en moyenne). Ce sont les données moyennes de la température potentielle pour les années 1961 à 2010. Pour ceux qui ont survécu jusqu'ici, ils peuvent être fier d'eux. On vient de réaliser le même boulot qu'un modèle météorologique, on prend une grosse équation qui fait peur, on se dit que ça va bien se passer, et on résout. Les valeurs calculées correspondent à peu près au modèle pour 50°N (à dextre donc). À la louche (c'est simplement pour "zoner" et situer un peu près avec des valeurs courantes, les calculs ne se voulaient pas représentatif d'un lieu et d'un moment spécifique), à la louche donc la valeur en surface est un peu près de 285 - 280 K, proche des 288 K calculés. À 850 hPa, la valeur se situe vers 285 - 290 K, proche des 291 K calculés. À 500 hPa, la valeur se situe vers 305 K, proche des 308 K calculés. À 300 hPa, la valeur se situe vers 315 - 320 K, proche des 322 K calculés. À 200 hPa, la valeur se vers 345 - 350 K, proche des 353 K calculés.
Pour ceux qui veulent du vocabulaire pour placer des mots dans un dîner de famille, les régions où les températures potentielles sont constantes avec l'altitude, les régions tropicales et polaires (visuellement, les courbes sont horizontales) sont les régions barotropes. Au contraires, les latitudes moyennes où la température potentielle varie rapidement pour une altitude donné (visuellement les courbes sont penchés) sont les régions baroclines.
Gradient thermique adiabatique sec
Pour les anglophones, on parle aussi de "dry adiabatic lapse rate" ou DALR (oh yeah ! ). Derrière cette expression barbare se cache simplement la notion de variation de température avec l'altitude. Nous allons voir à quel rythme la température peut décroître avec l'altitude si l'atmosphère était sèche et non convective. L'équation est la suivante :
dT / dz = - g / Cp
dT / dz = - 9.81 / 100
dT / dz = - 0.0098 °C.m-1
C'est un résultat qui a un côté remarquable. Cela implique que dans dans une atmosphère tout à fait sèche et neutre pour la convection, la température diminuera toujours de 10°C environ pour 1000 mètres ou bien de 1°C pour 100 mètres.
En clair, prenons une particule d'air sec qui part de la surface et qui soit forcé de grimper. Puisqu'elle s'élève, elle rencontre une pression qui diminue. Elle se détend alors, et donc se refroidit. Et bien, ce refroidissement s'effectue au rythme de 1°C par 100 mètres. C'est le gradient thermique adiabatique sec. C'est une manière de mesurer le fait que l'air chaud est en haut, et l'air froid en bas.
Dans l’atmosphère réelle, la température diminue beaucoup plus rapidement que le gradient thermique adiabatique sec. Ou dit autrement, si une parcelle d'air est forcé à s'élever (relief, convergence des vents, etc...) ; en s'élevant elle va se détendre et se dilater. Et en se détendant, elle va se refroidir, et devenir donc plus lourde que son environnement, et s'opposer donc au mouvement ascensionnel. L'air est donc stable à grande échelle pour une atmosphère sèche.
Cependant, certains jours d’Été, le sol peut surchauffer et la température peut atteindre un maximum en surface suffisant pour qu'il se mette en place de la convection sèche. Cela signifie que l'air, si il est forcé à s'élever, se refroidira moins rapidement que son environnement, restera donc plus léger et continuera à monter. Cette instabilité sèche, qu'on appelle suradiabatisme car on est au delà du gradient thermique adiabatique sec, est bien connu des planeurs et des piafs. Les jours de plein Soleil, ils s'en servent pour monter sans effort, en large cercle concentrique pour rester dans la colonne d'air chaud. Cette instabilité reste cependant toujours peu profonde, se confinant dans les 1000 ou 2000 premiers mètres de l'atmosphère, et elle est d'extension spatiale très limitée, de l'ordre de 100 mètres à 1 kilomètre. L'air est stable à grande échelle.
L'air humide
Il ne fallait guère espérer que les choses restent aussi simples. En effet, la condensation de l'eau (le passage de l'état vapeur à l'état liquide) est un processus qui libère de la chaleur, et l'évaporation (le passage de l'état liquide à l'état vapeur) absorbe de la chaleur. Ainsi, les variations des états de la vapeur d'eau jouent un rôle majeur dans les équilibres thermodynamiques. Pour la minute vocabulaire, on parle de chaleur latente pour désigner cette énergie. En effet cette chaleur ne modifie pas la température, à la différence de la chaleur sensible. C'est quelque peu contre intuitif, en général on associe a chaleur à la température. Pourtant, même une parcelle air avec une température assez basse peut être "chaud" car elle est bourrée de vapeur d'eau, et donc de chaleur latente. En quelque sorte, l'air humide contient plus d'énergie que l'air sec. La température est alors soumise non seulement à la pression -comme dit précédemment- mais aussi à la teneur en vapeur d'eau de la parcelle d'air considéré.
Il convient dans un premier temps d'expliciter brièvement les différents paramètres qui permettent de quantifier la vapeur d'eau. Il existe une foule de paramètres, mais nous nous focaliserons sur trois en particulier pour rester simple.
En premier lieu, on peut décompter simplement la masse de vapeur d'eau contenue dans l'atmosphère. C'est l'humidité spécifique, qui donne ainsi la masse de vapeur d'eau par kilogramme de masse d'air total (donc y compris la vapeur d'eau). Elle est souvent exprimée en grammes par kilogramme et non en kilogramme par kilogramme, les chiffres étant faibles. Pour donner un ordre de grandeur, dans une masse de un kilogramme d'air en Hiver, il y a environ 3 à 7 grammes de vapeur d'eau à la surface. En Été, c'est plus variable, mais nous sommes généralement entre 5 et 15 grammes de vapeur d'eau pour un kilogramme d'air pris à la surface.
En deuxième lieu, on peut mesurer la température à laquelle la vapeur d'eau condenserait. C'est le point de rosée. Intuitivement, on a tous déjà fait l'expérience du point de rosée. C'est par exemple le cas dans une cuisine en Hiver quand la buée se forme sur les vitres. Si l'eau condense, c'est que la température des fenêtres est inférieur au point de rosée de l'air ambiant. Il se passe la même chose avec une canette fraîche sorti du distributeur en plein air en été. En général, si la canette est vraiment fraîche, l'eau va condenser à sa surface. On pourrait imaginer une expérience où on aligne à l'ombre mais en plein air des canettes avec une température contrôlée au degré près. Ainsi, le point de rosée serait la température de la première canette où se produit la condensation. En pratique il existe des hygromètres où sondes à humidité qui permettent de mesurer le point de rosée sans devoir aligner les canettes.
Il y a enfin une autre mesure qui est la pression de vapeur. Comme dit, un gaz se caractérise par sa pression et sa température. Au lieu de chercher la température à laquelle la vapeur d'eau condense, on peut chercher la pression à laquelle l'eau condense pour une température donnée. C'est la tension de vapeur, qui se mesure comme toute pression en Pascals ou plus couramment en hectopascals. À 0°C la tension de vapeur est de 611 hPa environ. Et à 100°C, sans surprise, la tension de vapeur est de une atmosphère, 1000 hPa environ. C'est la raison pour laquelle une casserole d'eau porté à 100°C bout.
Il faut savoir que l'air peut contenir 6% à 7% plus de vapeur d'eau par degré environ, c'est la relation de Clausius-Clapeyron. Cela veut dire que l'air chaud peut potentiellement contenir plus de vapeur. C'est la raison pour laquelle les plus forts cumuls de pluies se rencontrent dans les régions tropicales, en Indonésie et en Inde en particulier, là où l'air peut contenir énormément de vapeur et donc donner des pluies torrentielles quand la vapeur se condense. C'est aussi une des raisons qui fait que le réchauffement climatique pose autant de problème.
 |
| Relation entre l'humidité spécifique et la tension de vapeur en fonction de la température. |
 |
| Diagramme psychrométrique |
Les deux graphiques présentent la même information. Pour le second, en partant de la température, en bas, on va chercher la courbe pour une saturation donnée (noté φ, phi, sur le deuxième diagramme, l'espèce de petite boucle toute mignonne). On peut alors ensuite lire sur l'axe de droite le rapport de mélange, qui est pratiquement égale à l'humidité spécifique. Sur le premier graphique, l'humidité spécifique est à gauche et la pression de saturation à droite.
Pour être pratique, un air avec un point de rosée à 10°C aura une humidité spécifique d'environ 7.7 grammes de vapeur d'eau au kilogramme d'air, et une tension de vapeur de 1230 Pascals environ. Un air à 20°C, avec une humidité relative de 50% aura une humidité spécifique de 7.3 grammes de vapeur d'eau au kilogramme d'air, et une tension de vapeur de 1170 Pascals environ. À 0°C et 100% d'humidité, l'air contient 3.8 grammes de vapeur au kilogramme d'air avec une tension de vapeur de 610 Pascals environ.
Pour les calculs d'air humide :
http://go.vaisala.com/humiditycalculator/5.0/
www.climatvisu.fr/Macro_excel/Humidite.xlsm
Pour le sujet, nous vous renvoyons plus spécifiquement à ce sujet sur notre blog : http://infometeobelgique.blogspot.fr/2016/06/vapeur-deau-et-rechauffement-climatique.html Depuis deux siècles, la teneur en vapeur de l'atmosphère a augmenté de 7% justement environ, ce qui provoque une "accélération" du cycle de l'eau. Cela se voit par exemple à des épisodes neigeux moins fréquents mais apportant plus de neige... Bref, l'air chaud peut contenir plus de vapeur d'eau, et l'air froid peut donc contenir moins de vapeur d'eau. Quand l'air est forcé à s'élever, il va donc se détendre et se refroidir. À un moment, il n'y aura plus de place pour la vapeur d'eau, qui va se mettre à condenser. Cette condensation va relâcher de la chaleur latente donc, qui va réchauffer la parcelle d'air. Ainsi, l'air ne se refroidir plus au rythme de 1°C par 100 mètres, mais à une valeur moindre (de l'ordre de 0.5°C à 0.6°C pour 100 mètres). Intuitivement, on devine déjà que la convection humide est un cas beaucoup plus courant que la convection sèche. Et c'est en effet le cas, la convection humide est à l'origine des orages, qui sont relativement fréquents, même en Hiver.
On va alors définir deux températures, la température potentielle équivalente θe et la température pseudo-potentielle du thermomètre mouillé θ'w.
Température potentielle équivalente : θe
Pour définir cette température, on va partir d'une parcelle d'air contenant de la vapeur d'eau. Puis on va imaginer que toute l'eau se condense et se transforme en eau liquide, et est éliminée. La condensation de l'eau va provoquer un échauffement de la parcelle d'air. Ainsi, la température va très fortement augmenter au cours du processus. Cela garde un côté "virtuel" et on ne verra jamais dans l’atmosphère un volume d'air où toute la vapeur d'eau se condense. Ce processus permet cependant de définir une nouvelle température, la température potentielle équivalente notée θe -thêta E-. Nous n'allons pas la définir précisément (si certains y tiennent : https://en.wikipedia.org/wiki/Equivalent_potential_temperature)
Le calcul de la θe est assez simple intuitivement. On calcule déjà la température potentielle Te. La vapeur d'eau, en passant de l'état gazeux à l'état liquide, libère de la chaleur. En effet, dans un gaz, les molécules sont "excités" et bougent en tout sens, alors que dans un liquide elles sont plus sages. Ainsi, en se condensant, la vapeur va rendre son énergie à l'air environnant. Pour les ordres de grandeurs, la condensation d'un gramme de vapeur d'eau pourra échauffer le kilogramme d'air qui le contient de 2.3°C à 2.4°C environ. Les changements d'états sont redoutables d'efficacité pour chauffer l'air ambiant, d'où l’importance de la chaleur latente. Ensuite, une fois connue la température potentielle, on la ramène au niveau de pression standard de 1000 hPa comme explicité précédemment.
Pour définir cette température, on va partir d'une parcelle d'air contenant de la vapeur d'eau. Puis on va imaginer que toute l'eau se condense et se transforme en eau liquide, et est éliminée. La condensation de l'eau va provoquer un échauffement de la parcelle d'air. Ainsi, la température va très fortement augmenter au cours du processus. Cela garde un côté "virtuel" et on ne verra jamais dans l’atmosphère un volume d'air où toute la vapeur d'eau se condense. Ce processus permet cependant de définir une nouvelle température, la température potentielle équivalente notée θe -thêta E-. Nous n'allons pas la définir précisément (si certains y tiennent : https://en.wikipedia.org/wiki/Equivalent_potential_temperature)
Le calcul de la θe est assez simple intuitivement. On calcule déjà la température potentielle Te. La vapeur d'eau, en passant de l'état gazeux à l'état liquide, libère de la chaleur. En effet, dans un gaz, les molécules sont "excités" et bougent en tout sens, alors que dans un liquide elles sont plus sages. Ainsi, en se condensant, la vapeur va rendre son énergie à l'air environnant. Pour les ordres de grandeurs, la condensation d'un gramme de vapeur d'eau pourra échauffer le kilogramme d'air qui le contient de 2.3°C à 2.4°C environ. Les changements d'états sont redoutables d'efficacité pour chauffer l'air ambiant, d'où l’importance de la chaleur latente. Ensuite, une fois connue la température potentielle, on la ramène au niveau de pression standard de 1000 hPa comme explicité précédemment.
Température pseudo-potentielle du thermomètre mouillé : θ'w
La méthode la plus simple pour comprendre, c'est vous, sortant de votre douche nu comme un ver, courant à travers la maison (voire dehors pour les plus expressifs) et ayant bien froid. À ce moment, vous faites un parfait un thermomètre mouillé. Pour comprendre, il faudra prendre le processus inverse de la condensation, qui est l'évaporation. L'air ambiant étant rarement tout à fait saturé, le déficit de saturation va permettre à l'eau liquide de s'évaporer. L'évaporation consommant de la chaleur, elle va refroidir la surface qu'elle quitte. C'est accessoirement le même principe pour le refroidissement par transpiration (ou en tirant la gueule pour nos amis à poils et à puces), ce qui fait que la θ'w est un très bon indicateur du stress thermique. Le dépassement des 35°C de θ'w durant plus de quelques heures est rapidement létal. Pour revenir à la θ'w, son calcul est assez complexe (cela nécessite d'itérer pour ceux à qui cela parle). Cependant, l'idée est bien de mesurer le refroidissement de l'air faisant suite à sa saturation par évaporation. C'est donc aussi une autre mesure de l'énergie de la parcelle d'air. Plus l'air est humide, moins il pourra se refroidir suite à une évaporation. Dans un brouillard, la θ'w est la même que la température de l'air, alors que dans un air très sec, la θ'w va baisser très fortement suite à l'évaporation d'une grande quantité d'eau. Ainsi, un air sec sera toujours plus "froid" qu'un air humide. Ensuite, une fois connue la température du thermomètre mouillé, on la ramène au niveau de pression standard de 1000 hPa.
La méthode la plus simple pour comprendre, c'est vous, sortant de votre douche nu comme un ver, courant à travers la maison (voire dehors pour les plus expressifs) et ayant bien froid. À ce moment, vous faites un parfait un thermomètre mouillé. Pour comprendre, il faudra prendre le processus inverse de la condensation, qui est l'évaporation. L'air ambiant étant rarement tout à fait saturé, le déficit de saturation va permettre à l'eau liquide de s'évaporer. L'évaporation consommant de la chaleur, elle va refroidir la surface qu'elle quitte. C'est accessoirement le même principe pour le refroidissement par transpiration (ou en tirant la gueule pour nos amis à poils et à puces), ce qui fait que la θ'w est un très bon indicateur du stress thermique. Le dépassement des 35°C de θ'w durant plus de quelques heures est rapidement létal. Pour revenir à la θ'w, son calcul est assez complexe (cela nécessite d'itérer pour ceux à qui cela parle). Cependant, l'idée est bien de mesurer le refroidissement de l'air faisant suite à sa saturation par évaporation. C'est donc aussi une autre mesure de l'énergie de la parcelle d'air. Plus l'air est humide, moins il pourra se refroidir suite à une évaporation. Dans un brouillard, la θ'w est la même que la température de l'air, alors que dans un air très sec, la θ'w va baisser très fortement suite à l'évaporation d'une grande quantité d'eau. Ainsi, un air sec sera toujours plus "froid" qu'un air humide. Ensuite, une fois connue la température du thermomètre mouillé, on la ramène au niveau de pression standard de 1000 hPa.
En pratique
La θe et la θ'w expriment la même idée. La différence entre les deux est plus de l'ordre de l'habitude et de la pratique, mais l'information convoyée par ces deux mesures est la même et elles occupent la même place dans les équations. MétéoFrance par exemple privilégie la θ'w pour ces prévisions, alors qu'en météorologie tropicale, et plus particulièrement pour l'étude des cyclones, la θe est plus fréquemment utilisée, surtout outre Atlantique. Certains sites internet proposant les sorties des modèles calculent à la fois la θ'w et la θe mais c'est plus pour faire du volume pas cher que pour une autre raison. En théorie, notamment pour des calculs d'entropie, il peut y avoir des arguments pour préférer un paramètre à l'autre. En pratique et en opérationnel cependant, cela ne fait aucune différence, les cartes de la θ'w et de la θe étant identique. Les cartes peuvent se trouver à différentes adresses, ici par exemple :
http://www1.wetter3.de/animation.html
sous le nom de pseudopot. temperature
ou ici :
http://www.wetterzentrale.de/topkarten/fsavneur.html
sous le nom de Pot. Äquiv. Temp.
Le paramètre est généralement étudié à 850 hPa, c'est-à-dire vers 1500 mètres d'altitude. On s'affranchit ainsi de l'influence de la surface, tout en restant en basses couches. C'est à ce niveau que l'on va rechercher les anomalies chaudes et froides, qui influeront notre temps. Il est important ici de préciser qu'on parle d'anomalies spatiales. c'est-à-dire si on a deux patates d'air de températures différentes qui se frottent. Par exemple, une masse d'air à 9°C qui frotte une masse d'air à 5°C sera une anomalie chaude, mais une masse d'air à 13°C qui frotte un air à 9°C sera aussi une anomalie chaude, la masse d'air à 9°C étant alors la masse d'air froide... Il n'y a aucune valeur absolue, juste des valeurs relatives l'une à l'autre.
On peut ainsi définir les masses d'air et les fronts. Une masse d'air présente une certaine homogénéité avec une θ'w ou une θe sensiblement similaire. Ces masses d'airs peuvent alors s'affronter. Quand une masse d'air chaud progresse et l'emporte sur une masse d'air froid, on parle de front chaud. Quand une masse d'air froid progresse et l'emporte sur une masse d'air chaud, on parle de front froid. Ici même : http://infometeobelgique.blogspot.fr/2016/02/bande-etroite-de-front-froid.html nous avions détaillé le cas d'un front froid.
Schématiquement, cela ressemble à ceci :
Les lignes noires symbolisent le champ de pression, avec un minimum au centre (une dépression donc). Les plages de couleurs symbolisent la température de l'air. Les flèches marrons symbolisent le vent. Et la grosse flèche verte symbolise le déplacement général de la dépression. Et dans la vraie vie :
La carte présente le champ de pression en contours blancs et la θe en couleurs. Il s'agit de la situation de Décembre 2013, avec le creusement successifs de multiples dépressions (dont, à la toute fin, la tempête Dick qui avait gentiment secoué l'Europe du Nord-Ouest
 |
| Infographie que nous avions construite après la tempête Dick de fin Décembre 2013. |
L'important est bien de délimiter les patates d'air qui sont plus chaudes ou plus froides que l'environnement. Ce sont les anomalies chaudes, qui sont souvent associés à des frontogenèses (formation des fronts) et des cyclogenèses (creusement des cyclones). Il ne faut pas chercher une valeur absolue qui définit si une masse d'air est douce ou non, c'est toujours relativement aux voisins. Deux exemples, un en Juillet 2010 et un en Décembre 2010. Dans les deux cas, une petite dépression se creuse au large du Golfe de Gascogne et amène en flux de Sud-Ouest de l'air relativement doux. Cependant, en Décembre, l'air "doux" qui est advecté vers le Nord est pratiquement aussi frais que l'air froid qui s'engouffre à l'arrière de la dépression en Juillet...
 |
| Situation du 11 Juillet 2010 à 00Z. Source : http://www1.wetter3.de/animation.html |
 |
| Situation du 08 Décembre 2010 à 00Z. Source : http://www1.wetter3.de/animation.html |
Les cartes de θ'w et θe sont donc très étudiées par les météorologues pour prévoir le temps. Elles permettent de suivre les masses d'airs, de voir où celles-ci s'affrontent.
Pour les autres de grandeurs malgré tout, les valeurs communes de θ'w sont habituellement vers les 2°C à 6°C dans l'air froid d'Hiver, entre 11°C et 15°C dans l'air chaud d'Hiver, et peut descendre au plus froid vers les -5°C. En Été, l'air chaud est vers 13°C à 19°C, les plus fortes valeurs étant vers 20°C à 23°C. L'air froid d’Été quand à lui est généralement vers 8°C à 12°C.
De plus, elles sont utiles pour la prévision de la convection. L'air chaud de surface est favorable à de la convection. Comme nous l'avons mentionné, l'instabilité sèche est rare alors que l'instabilité humide est plus courante. Les régions où les températures atteignent un maximum, surtout en Été, sont généralement les régions les plus favorables à des déclenchements convectifs. Dans ce cas il peut parfois être utile d'étudier la θ'w ou la θe à un niveau inférieur. C'est particulièrement le cas dans les épisodes méditerranéens. Il est fréquent de regarder où se situe l'advection la plus chaude à des niveaux inférieurs, vers 950 ou 925 hPa (vers 500 et 800 mètres respectivement). De manière générale, la position spatiale et la profondeur du maximum d'advection sont des indicateurs importants pour la convection.
Un autre intérêt pratique de la θ', et seulement de la θ'w cette fois-ci, est une indication de la limite-pluie neige. L'iso 0°C de la θ'w est généralement une bonne indication de l'altitude de la limite pluie-neige. Un truc empirique est de mettre la limite pluie-neige 200 ou 300 mètres sous l'isotherme 0°C en situation stable, entre 500 et 800 mètres sous l'isotherme 0°C en situation instable. Une autre technique est de considérer effectivement l'iso θ'w 0°C, qui est en toute logique sous l'isotherme 0°C.
Conclusion
En avant les histoires...Complément : l'entropie
Puisque le mot a été lâché, il va falloir l'expliquer. Pour ceux qui ont en sainte horreur la physique, vous pouvez cependant passer votre chemin. Ce sera sans doute la partie la plus dense de cet article, il va falloir être fort psychologiquement. L'entropie donc... ( pour ceux qui non pas peur du mal de crâne : https://fr.wikipedia.org/wiki/Entropie_%28thermodynamique%29 et https://fr.wikipedia.org/wiki/Gaz_parfait#Entropie). En gros, l'entropie représente l'état de désordre d'un système. Pour faire simple, prenons un château de cartes et deux frères. Le plus jeune prend le temps d'édifier un château, transpire, tire la langue, et construit un magnifique un ouvrage. L'aîné arrive, rit et souffle sur l'ouvrage (car c'est bien connu, il faut toujours que les grands frères courent sur le haricot des petits frères...). Et bien, l'entropie du château de carte est très faible, car le système est ordonné. Par contre, quand le château vole et s'envole au vent mauvais, son entropie augmente. Les cartes se retrouvent dispersées en tout sens dans toute la pièce, les unes de recto, les autres de verso, certaines appuyées sur la tranche contre le mur ou le radiateur. Bref, il y en a partout, dans tout les sens. Même si ce n'est pas en rapport direct avec le propos, nous pouvons noter qu'il est plus facile pour un système d'avoir une forte entropie, qu'une faible entropie. Il faut "travailler" pour réduire l'entropie du système. Et un système tend à se désordonner. C'est le deuxième principe de la thermodynamique, qui en gros dit que tout système -et l'Univers en général- tend vers le bordel maximum (soit dit en passant, c'est généralisable à tout système, même non physique... La prochaine fois que vous vous rendrez compte que c'est le bordel sur le ring de Bruxelles ou dans votre entreprise, vous saurez que c’est le deuxième principe de la thermodynamique). Une autre manière de voir les choses peut être la suivante. L'entropie indique la "qualité" d'une énergie en quelque sorte.Quel est donc le rapport avec la température potentielle ? Et bien, parlons déjà d'air sec (et oui, pour ne pas vous laisser mariner plus longtemps, sachez qu'on parler de l'air humide après...). La température potentielle est une mesure de l'entropie de l'air sec. Elle est bien pratique pour montrer que l'air froid est au fond du bocal, mais elle a une origine tout autre, et elle a bien plus d'intérêt.
Nous n'allons pas démontrer comment passer de l'entropie à la température potentielle Note 2. Le fait est que la température potentielle est en quelque sorte une mesure de l'entropie de l'air sec.
En général, les évolutions de l'atmosphère sont adiabatiques. Et un mot compliqué de plus (on ne va pas les compter sinon on n'a pas fini...). Pour ceux qui seraient un peu hellénistes aussi à leurs heures perdues, adiabatique vient du grec ἀδιάϐατος, infranchissable. Le mot en lui-même est composé de trois éléments, le préfixe ἀ- qui est le préfixe privatif (agnostique, adamantin, etc..), διά qui exprime l'idée de "à travers" (diarrhée, couler à travers), et βαίνω qui signifie aller, venir (et qui a justement donné par évolution du "b doux" grec vers le v, le verbe venir par le latin venio, et vive les assonances). Bref, donc, adiabatique. La phrase consacrée est de dire qu'il n'y a pas d'échanges de chaleur. Le système n'échange pas de chaleur avec son environnement. C'est une hypothèse importante et qui est en général valable pour l'air sec. En effet, l'air est un très mauvais conducteur thermique (ou dit autrement, c'est un bon isolant thermique, d'où le double et le triple vitrage). De plus, l'air est quasi exclusivement chauffé depuis la base. La surface terrestre absorbe la chaleur du Soleil alors que l’atmosphère la laisse passer. Sur l'échelle de quelques jours, l'air subit donc peu les influences des échanges de chaleur.
De plus, les évolutions de l'air sont généralement réversibles. Cela veut dire qu'il n'y a pas hausse de l'entropie pour l'air. Ce n'est jamais tout à fait vrai en pratique pour l'air mais là aussi ce n'est pas tout à fait une mauvaise hypothèse.
Dans la vie courante, ce n'est jamais le cas par contre. Prenons une voiture ou un vélo ou une caisse à savon (voire une longboard pour les plus téméraires) au sommet d'un " V ", avec une descente suivi d'une montée approximativement équivalente. Si on laisse le véhicule aller son train, tout le monde comprend bien qu'il s'arrêtera à mi-pente dans la montée et n'arrivera jamais au sommet en face. Il y a donc irréversibilité car l'engin n'a pas réussi à revenir à son altitude initiale. En effet, lors de la descente, l'entropie du système augmente. Les frottements en particulier provoquent un échauffement. Cet chaleur part réchauffer les petits oiseaux et ne sert nullement à faire avancer l'engin. L'équipage perd donc de la vitesse sous forme de chaleur, et cette vitesse lui manquera pour grimper la pente qui se présente en face. Les frottements sont une source majeur d'irréversibilité. L'air cependant, en altitude, frotte peu et cette force est négligeable.
Ces deux hypothèses, à savoir que les évolutions de l'air libre sont adiabatiques et réversibles, impliquent que si on laisse une particule d'air vivre sa vie de particule elle conservera son entropie. Et comme la température potentielle est une mesure de cette entropie, on devine l'intérêt de cette grandeur.
En effet, la température potentielle est une grandeur conservée. Elle est donc en quelque sorte une "étiquette" qu'on peut attacher à une particule d'air. C'est donc une grandeur bien pratique.
Notes
1. Pour ceux qui voudraient tenter l'expérience, les erreurs de mesures risquent d'être largement supérieures à la valeur recherchée... L'idéal serait d'avoir un tube d'un litre voire de deux litres, tout en longueur et avec une très petite ouverture (l'aide d'un entonnoir est alors bienvenu...) ↩
2. Si nous avons quelques fanatiques des mathématiques pures et dures (plus dures que pures...), l'équation se démontre ainsi. En acceptant les résultats de Wikipédia : https://fr.wikipedia.org/wiki/Gaz_parfait#Entropie (rassurez-vous, on peut), notons s, l'entropie du système. D'après le deuxième principe de la thermodynamique revisité pour les gaz parfaits donc :
Δs = Cp * log ( T2 / T1 ) – r * log ( P2 / P1 )
En supposant l'évolution adiabatique réversible, donc isentropique, Δs est nul ( comme nous !) :
Cp * log ( T2 / T1 ) – r * log ( P2/P1 ) = 0
En travaillant au corps les logarithmes :
Cp * log ( T2 / T1 ) = r * log ( P2 / P1 )
log ( T2 / T1 ) = ( r / Cp ) * log ( P2 / P1 )
T2 / T1 = ( P2 / P1 ) ^ ( r / Cp )
T2 = T1 * ( P2 / P1 ) ^ ( r / Cp )
Par convention, T2 est la température potentielle et P1 est une pression de référence placé à 1 000 hPa.



Aucun commentaire:
Enregistrer un commentaire
Remarque : Seul un membre de ce blog est autorisé à enregistrer un commentaire.